「リーマン予想の証明」はドイツの数学者・リーマンが1859年に提起し、160年以上たった現在も解かれていない数学史上最大の難問であり、1億円の懸賞金がかけられている。「リーマン予想」は、「一見無秩序な数列にしか見えない“素数”がどのような規則で現れるか」という問いに答えるための重要な鍵である。「素数を現す方程式、ゼータ関数の非自明なゼロ点全てが一直線上に並ぶことの証明」がリーマン予想の証明であり、創造主の暗号とも言われる素数の謎、その証明に天才数学者たちが挑戦し続けている。
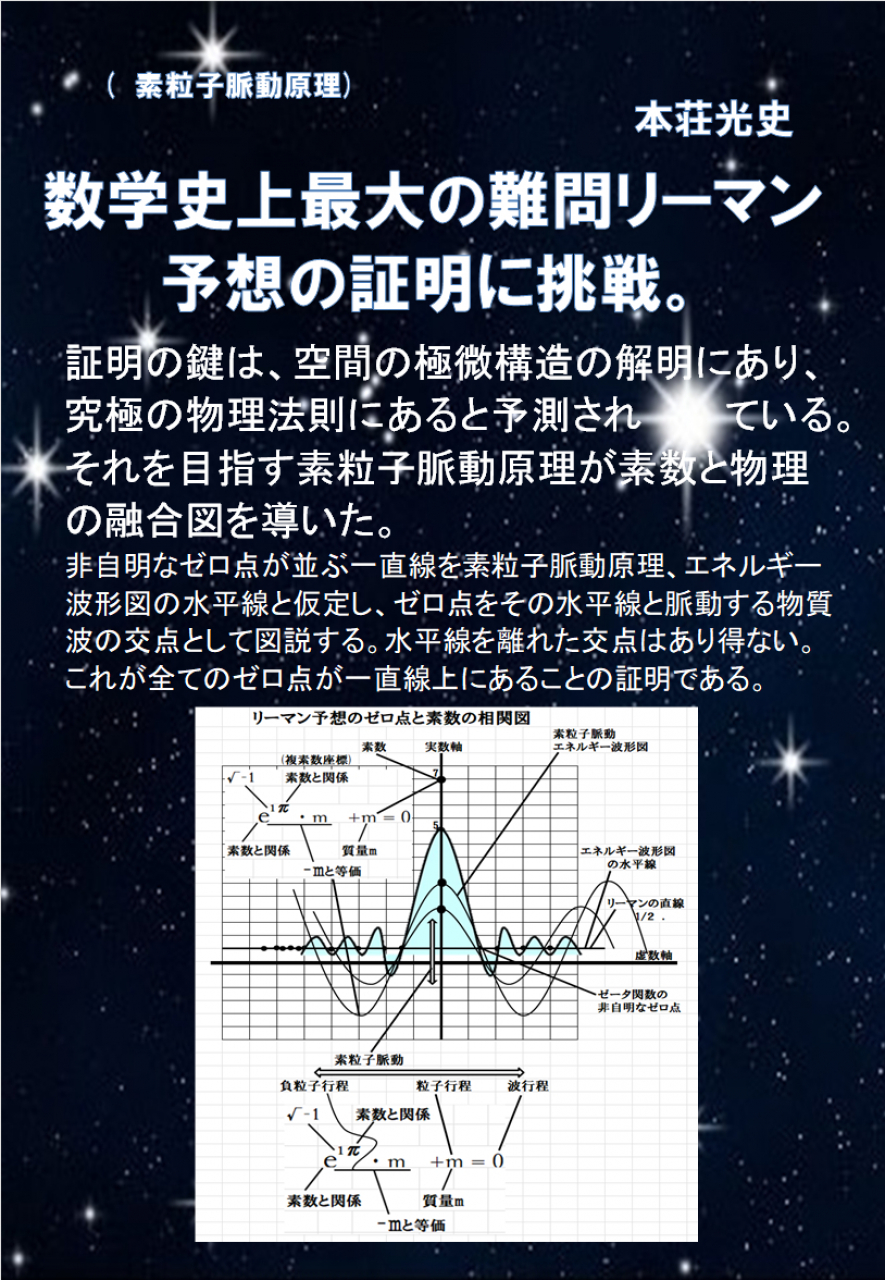
理論物理学への大統一理論として提唱している仮説「素粒子脈動原理」に基づいて発想した素数・物理融合図はリーマン予想の証明に最接近しているように見受けられる。 素数・物理融合図は複素数座標で現され、複素数座標を90°回転させて虚数軸を水平にしている。さらに、リーマン予想のゼロ点が並ぶ一直線を、素粒子脈動原理を現したエネルギー波形図の水平線として現している。この水平線は真空空間のエネルギー大気(エーテル?)のエネルギー濃度を現し、波形は物質波を現している。その物質波の頂点を素数と対応させ、物質波と水平線との交点をリーマン予想の非自明なゼロ点として現している。この物質波は量子力学のシュレーディンガー方程式とハイゼンベルグの行列による方程式によって現されており、素数の配列を現したゼータ関数と相関している。さらに、リーマン予想の証明に最も近い人物とされているアラン・コンヌ氏の言葉「リーマン予想の鍵はミクロ空間の非可換幾何学にある。」にも相関している。さらに、ド・ブランジュ氏の「リーマン予想の鍵は空間の光のスペクトル構造」にも相関している。 物質波と水平線との交点として現したリーマン予想のゼロ点は水平線以外には存在しない、水平線を離れた交点はありえない。 ゼータ関数の波形の線上で、ゼロ点だけが実数で水平線(3次元空間)上にある。水平線を離れた線状の点は全て虚数である。 交点(ゼロ点)は水平線上に無限に存在し、ゼロ点毎にゼロ点を通過する物質波(光)は光の波長変化に対応した虹色のスペクトルにも対応している。この物質波は理論物理学の核力・重力・電磁気力を現す大統一理論でもあり、素数の配列に対応したリーマン予想のゼロ点との相関図を現している。
・量子力学におけるシュレーデインガー方程式は、フーリエ変換によって複雑な波動方程式の波形を無限個の単純な正弦波群に置き換えている。
同様に、素数を現すゼータ関数の複雑な波形を無限個の単純な正弦波群に置き換える。正弦波と水平線の交点(非自明なゼロ点)は全て水平線上にあり、水平線(リーマンの直線)から離れた交点は存在しない。これがリーマン予想の証明である。
・物理学の大統一理論からのリーマン予想へのアプローチは初めての試みだと考えられる。ペレルマンによるポアンカレ予想の難問解決も微分幾何学や物理からのアプローチであった。数学からの挑戦を全てはねつけていた難攻不落のリーマン予想の証明も物理からの挑戦が大きな突破口となる可能性がある。
| はじめに |
| 第1章 数学史上最大の難問、素数 |
| [1] オイラー方程式による素数・物理相関図。 |
| [2] 素粒子脈動原理が導いた素数・物理融合図 |
| [3] 数学史上最大の難問「リーマン予想の証明」とは |
| [4] 暗黒エネルギーと素数の関係。 |
| 第2章 リーマン予想の証明 |
| [1] 素数の謎、数学史上最大の難問、リーマン予想の証明に挑戦 |
| [2] 素粒子脈動原理がリーマン予想証明の扉を開く |
| [3] リーマン予想の新解釈。ゼロ点は全て一直線との交点 |
| [4] 第一級数学者の予測と脈動原理解釈との一致 |
| [5] 素数・物理融合図が真理であると予感させるもの |
| [6] 電子書籍の表紙 |
| 第3章 素粒子脈動原理 |
| [1] 素粒子脈動原理の基礎概念 |
| [2] 素粒子が超高速で脈動しているエネルギーの塊 であると仮定する根拠。 |
| [3] 素粒子脈動原理が解く理論物理学の諸概念(1~33) |